Cos 2x O O tan 2xFree trigonometric equation calculator solve trigonometric equations stepbystep This website uses cookies to ensure you get the best experience ByQII i) Express the equation 3 sin = cos , in the form tan = k and solve the equation for 00 180 ii) Solve the equation 3 sin 2 x = cos 2x for O s x g 180 21 41 S15 / 13 / Q4 4 le tasz Q12 i) Prove the identity( for C) S x < 2n ii) Hence solve the equation W15 / 12 / Q4 1 3 sin e tan 94=0 can be expressed as Q13

Tan2x ただの悪魔の画像
Sin 2x tan 2x formula
Sin 2x tan 2x formula-Solve for x sin(2x)tan(x)=2 Move to the left side of the equation by subtracting it from both sides Since is on the right side of the equation, Take the inverse sine of both sides of the equation to extract from inside the sineDouble angle formulas We can prove the double angle identities using the sum formulas for sine and cosine From these formulas, we also have the following identities sin 2 x = 1 2 ( 1 − cos 2 x) cos 2 x = 1 2 ( 1 cos 2 x) sin x cos x = 1 2 ( sin 2 x) tan 2 x = 1 − cos 2 x 1 cos 2 x



Tan2x 1 ただの悪魔の画像
In this video you will learn how to verify trigonometric identitiesverifying trigonometric identitieshow to verify trig identitieshow to verify trigonometric There's a very cool second proof of these formulas, using Sawyer's marvelous ideaAlso, there's an easy way to find functions of higher multiples 3A, 4A, and so on Tangent of a Double Angle To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² ATRIGONOMETRY LAWS AND IDENTITIES DEFINITIONS sin(x)= Opposite Hypotenuse cos(x)= Adjacent Hypotenuse tan(x)= Opposite Adjacent csc(x)=
Sin 2x = (2tan x) /(1 tan 2 x) Therefore, the sin 2x formula in terms of tan is, sin 2x = (2tan x) /(1 tan 2 x) Great learning in high school using simple cues Indulging in rote learning, you are likely to forget concepts With Cuemath, you will learn visually and be surprised by the outcomesProof Half Angle Formula tan (x/2) Product to Sum Formula 1 Product to Sum Formula 2 Sum to Product Formula 1 Sum to Product Formula 2 Write sin (2x)cos3x as a Sum Write cos4xcos6x as a Product Prove cos^4 (x)sin^4 (x)=cos2x Prove sinxsin (5x)/ cosxcos (5x)=tan3xThe double angle formulas can be derived by setting A = B in the sum formulas above For example, sin(2A) = sin(A)cos(A) cos(A)sin(A) = 2sin(A)cos(A) It is common to see two other forms expressing cos(2A) in terms of the sine and cosine of the single angle A Recall the square identity sin 2 (x) cos 2 (x) = 1 from Sections 14 and 23
Transcript These formulas can be derived using x y formulas For sin 2x sin 2x = sin (x x) Using sin (x y) = sin x cos y cos x sin y = sin x cos x sin x cosTan double angle formula;Problem Set 53 Double Angle, Half Angle, and Reduction Formulas 1 Explain how to determine the reduction identities from the doubleangle identity cos(2x) = cos2x−sin2x cos ( 2 x) = cos 2 x − sin 2 x 2 Explain how to determine the doubleangle formula for tan(2x) tan ( 2 x) using the doubleangle formulas for cos(2x) cos




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
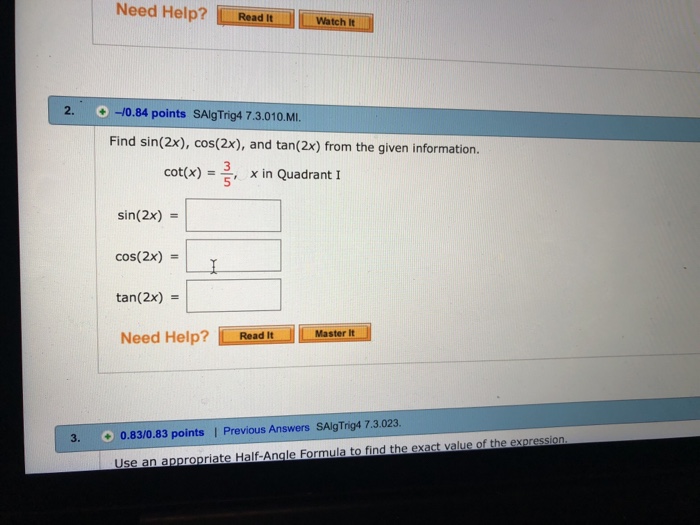



Solved Need Help Readt Watch It 2 10 84 Points Saigtrig4 Chegg Com
Get an answer for 'Prove tan^2x sin^2x = tan^2x sin^2x' and find homework help for other Math questions at eNotesTan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1Answer (1 of 3) 1sin^2x=1(1cos^2x) = 2cos^2x 1sin^2x= 2 cos^2x(1) Answer



Tan2x 1 ただの悪魔の画像




Tan2x ただの悪魔の画像
Legend x and y are independent variables, ;Get an answer for '`tan(2x) 2cos(x) = 0` Find the exact solutions of the equation in the interval 0, 2pi)' and find homework help for other Math questions at eNotesThe trigonometric formulas like Sin2x, Cos 2x, Tan 2x are popular as double angle formulae, because they have double angles in their trigonometric functions For solving many problems we may use these widely The Sin 2x formula is \(Sin 2x = 2 sin x cos x\) Where x is the angle Source enwikipediaorg Derivation of the Formula



What Is Integral Of Sin2x Tan2x Quora



Points Or No Points Maths Sl Ib Survival
Derivative Of sin^2x, sin^2(2x) – The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable Common trigonometric functions include sin(x), cos(x) and tan(x) For example, the derivative of f(x) = sin(x) is represented as f ′(a) = cos(a) f ′(a) is the rate of changeTrigonometry Formulas Involving Triple Angle Identities The triple of the angle x is presented through the below few trigonometryCalculus Calculus questions and answers 12 Find sin 2x, cos2x, and tan 2x if tanx= and x terminates in quadrant IV 5 0/0 님 sin 2x II 0 х Х $ ?




Cos2x 1 Sin2x Tan Pi 4 X Double And Half Angle Identity Youtube




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
Use tan x=sinx/cos x, sin 2x = 2 sin x cos x and cos 2x = cos^2xsin^2x, for the right hand side expression 2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x) =2 sin x cos x/(cos^2xsin^2x) =(sin 2x)/(cos 2x)=tan 2x Proofs for sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x Use Area of a triangleABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the triangle ABC of a unitRewrite tan(2x) tan ( 2 x) in terms of sines and cosines Substitute u u for sin(2x) sin ( 2 x) Add − u cos(2x) u cos ( 2 x) to both sides of the equation Factor u u out of 2u u cos(2x) 2 u u cos ( 2 x) Tap for more steps Factor u u out of 2 u 2 u Factor u u out of u cos ( 2 x) u cos ( 2 x)Cosine 2X or Cos 2X is also, one such trigonometrical formula, also known as double angle formula, as it has a double angle in it Because of this, it is being driven by the expressions for trigonometric functions of the sum and difference of two numbers (angles) and related expressions Let us start with the cos two thetas or cos 2X or cosine




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




View Question Find Sin 2x Cos 2x And Tan 2x From The Given Information Tan X 1 2 Cos X 0
Formula $\sin{2\theta} \,=\, 2\sin{\theta}\cos{\theta}$ A trigonometric identity that expresses the expansion of sine of double angle in sine and cosine of angle is called the sine of double angle identity Introduction Let theta be an angle of a right triangle, the sine and cosine functions are written as $\sin{\theta}$ and $\cos{\theta}$ respectivelySin 2x, Cos 2x, Tan 2x is the trigonometric formulas which are called as double angle formulas because they have double angles in their trigonometric functions Let's understand it by practicing it through solved example Best Answer #2 10 Find sin 2x, cos 2x, and tan 2x from the given information tan x = −1/2 , cos x > 0 In trigonometry, the tangent halfangle formulas relate the tangent of one half of an angle to trigonometric functions of the entire angle They are as follows




Tan2x ただの悪魔の画像



What Is Integral Of Sin2x Tan2x Quora
Double Angle Formulae Trigonometry Identities Sin2x, Cos2x & Tan 2x Class 11 Chapter 3 @StudY LoveR MeenA Double Angles Prove this Trigonometric IdentiQuestion 9671 Find sin 2x, cos 2x, and tan 2x from the given information sec x = 4, x in Quadrant IV sin 2x = cos 2x = tan 2x = Answer by Theo() (Show Source)(a) tan (3x °) = 2 3, (6) (b) 2 sin2 x cos2 x = 9 10 (4) (Total 10 marks) 3 Solve, for 0 ≤ θ < 2π, the equation sin2 θ = 1 cos θ , giving your answers in terms of π (Total 5 marks) 4 (a) Show that the equation 5 cos2 x = 3(1 sin x) can be written as 5 sin 2 x 3 sin x – 2 = 0 (2)




Tangent Half Angle Formula Wikipedia



What Is The Formula Of Tan2x Quora
Formulas from Trigonometry sin 2Acos A= 1 sin(A B) = sinAcosB cosAsinB cos(A B) = cosAcosB tansinAsinB tan(A B) = A tanB 1 tanAtanB sin2A= 2sinAcosA cos2A= cos2 A sin2 A tan2A= 2tanA 1 2tan A sin A 2 = q 1 cosA 2 cos A 2 In Trigonometry Formulas, we will learn Basic Formulas sin, cos tan at 0, 30, 45, 60 degrees Pythagorean Identities Sign of sin, cos, tan in different quandrants Radians Negative angles (EvenOdd Identities) Value of sin, cos, tan repeats after 2π Shifting angle by π/2, π, 3π/2 (CoFunction Identities or Periodicity Identities)Identities related to sin 2x, cos2x, tan 2x, sin3x, cos3x, and tan3x by 1 Sin 2x = Sin 2x = sin (2x)=2sin (x) cos (x) Sin (2x) = 2 * sin (x)cos (x) Proof To express Sine, the formula of "Angle Addition" can be used sin (2x) = sin (xx) Since Sin (a b) = Sin (a)



What Is The Value Of Sin 2x In Terms Of Tan X Quora
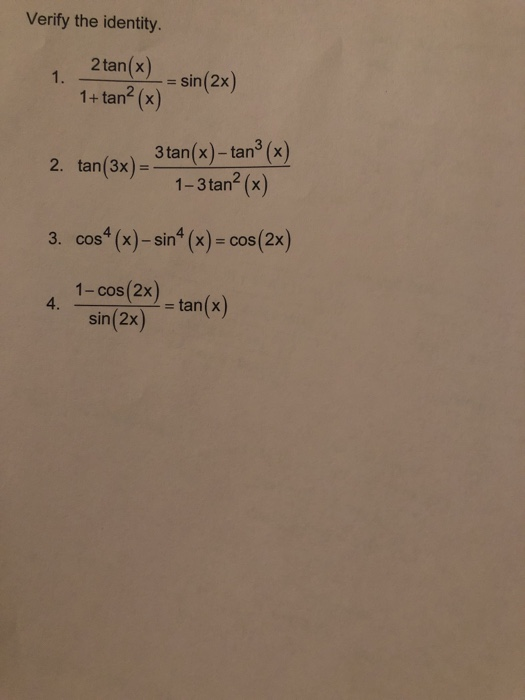



Solved Verify The Identity 2tan X Sin 2x 1 Tan2 X 2 Chegg Com
Cos (2x) = cos 2 (x) sin 2 (x) = (1 tan 2 x)/(1 tan 2 x) cos (2x) = 2cos 2 (x) 1 = 1 2sin 2 (x) tan (2x) = 2tan(x)/ 1 tan 2 (x) sec (2x) = sec 2 x/(2 sec 2 x) cosec (2x) = (sec x • cosec x)/2;To find the value of sin2x × Cos 2x, the trigonometric double angle formulas are used For the derivation, the values of sin 2x and cos 2x are used From trigonometric double angle formulas, Sin 2x = 2 sin x cos x ———— (i) And, Cos 2x = Cos 2 x − Sin 2 x = 2 cos 2 x − 1 ———— (ii) Since Sin 2 x Cos 2 x = 1Double angle formulas are called "double" angle because they involve trigonometric functions of double angles like sin 2x or cos 2x In other words, when we use the formula, we're doubling the angle These formulas allow you to rewrite a double angle expression like sin 2x and cos 2θ into an expression with a




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube




Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11
Formulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angle double of the angle present in their formulas Sin 2x Formula Sin 2x formula is 2sinxcosx Image will be uploaded soon Sin 2x =2 sinx cosx Derivation of Sin2x Formula Before going into the actual proofD is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4For each of the three trigonometric substitutions above we will verify that we can ignore the absolute value in each case when encountering a radical 🔗 For x = asinθ, x = a sin θ, the expression √a2 −x2 a 2 − x 2 becomes √a2−x2 = √a2−a2sin2θ= √a2(1−sin2θ)= a√cos2θ= acosθ = acosθ a 2 − x 2 = a 2 − a 2




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com
2 Answers2 tan(2x) = 2tanx 1 − tan2x = 2( − 4 / 3) 1 − ( − 4 / 3)2 = − 8 / 3 1 − 16 / 9 = − 24 − 7 = 24 7 tan(2x) = sin(2x) cos(2x) = − 24 / 25 − 7 / 25 = 24 7 If one is having difficulty with a problem like this, then perhaps going back to the original principles would be prudent Using the sin law we have sin2θ 2sinθQuestion Find sin 2x, cos 2x, and tan 2x from the given information sin x = 5/13, x in Quadrant III sin 2x = cos 2x= tan 2x = Find sin 2x, cos 2x, and tan 2x from the given information tanx= 1/4 , cosx > 0 sin 2x = cos 2x = Tan 2x = Find sin 2x, cos 2x, and tan 2x from the given information sin x = 5/13, x in Quadrant I sin 2x = cos 2xRecall that math\sin x\cos x=\dfrac{1}{2}\sin2x=\dfrac{1}{2}\dfrac{2\tan x}{1\tan^2x}/math and that math\sin^2x=\dfrac{\sin^2x}{\cos^2x\sin^2x}=\dfrac{\tan^2x




Cos 2x Formula Derivation Examples What Is Cos 2a Formula



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora
• take the Pythagorean equation in this form, sin2 x = 1 – cos2 x and substitute into the First doubleangle identity cos 2x = cos2 x – sin2 x cos 2x = cos2 x There are easier equations to the halfangle identity for tangent equation tan x/2 = sin x/ (1 cos x) 1st easy equation tan x/2 = (1 cos x) /sin x 2nd easy equation True Start with the well known pythagorean identity sin^2x cos^2x = 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identityFormula sin 2 θ = 2 tan θ 1 tan 2 θ A trigonometric identity that expresses the expansion of sine of double angle function in terms of tan function is called the sine of double angle identity in tangent function




Tan2x ただの悪魔の画像
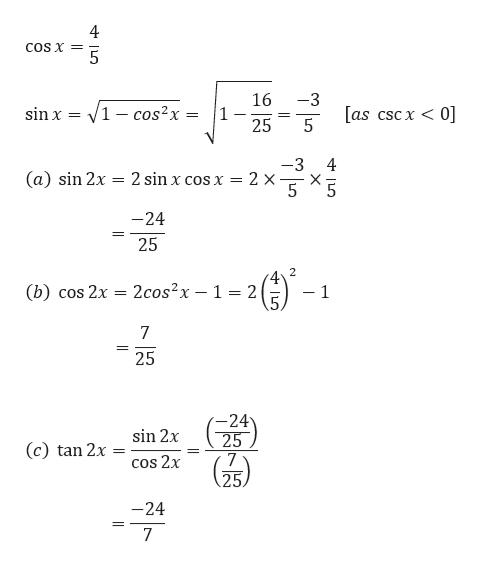



Answered If Cosx 4 5 Cscx 0 Then Sin 2x Bartleby



What Is The Formula Of Tan2x Quora




Example 14 Show Tan 3x Tan 2x Tan X Tan 3x Tan 2x Tan X




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube




Sin 2x Formula What Is Sin 2x Formula Examples




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Solved Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com




bestpictjcry Tan 2x Tan 2x
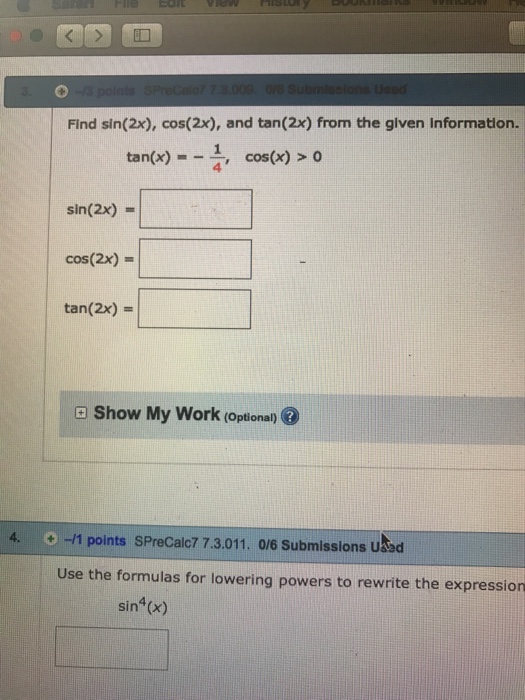



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



What Is The Formula Of Tan2x Quora



Tan2x 1 ただの悪魔の画像




Day 3 Hw 1 To 2 Find Sin2x Cos2x And Tan2x Given One Trig Value And The Quadrant Youtube




上 Tan2x Identity ただの悪魔の画像




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Sin2x Cos2x 1 Proof




Calculate Sin2x Cos2x And Tan2x For Given Tanx In Quadrant 2 Youtube




Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube




How To Solve Tan 2xsin 2x Tan 2x Sin 2x Trigonometry Trigonometric Identities Youtube




Maths Lover Maths Lover Added A New Photo
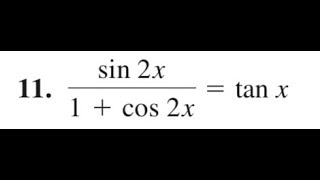



Verify Sin 2x 1 Cos 2x Tan X Youtube




Cos2x Sin2x 1 1 Tan2x Sec2x Cot2x 1 Csc2x Cofunction



Tan2x ただの悪魔の画像




Integrate Sec 2x Method 2




Trigonometric Identity 1 Cos2x Sin2x 1 Cos2x Sin2x Tanx Youtube
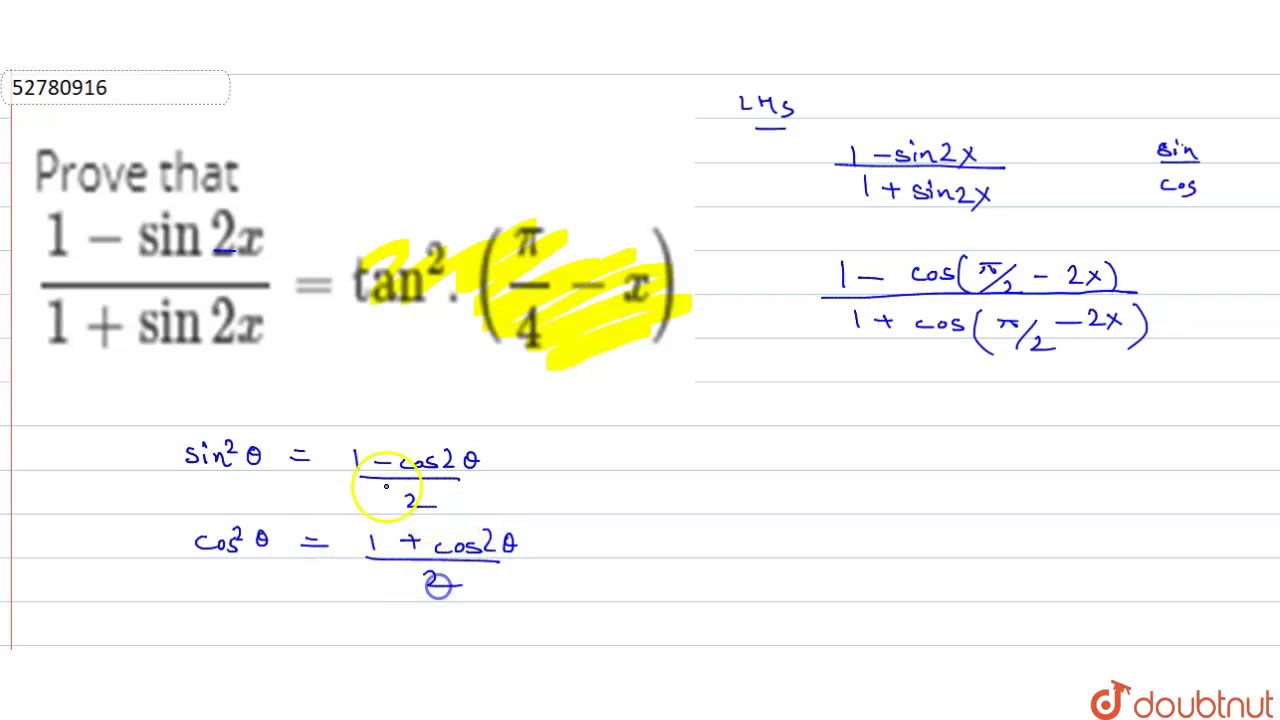



Prove That 1 Sin 2x 1 Sin 2x Tan 2 Pi 4 X Youtube




Tan 2x Sin 2x Tan 2xsin 2x Wyzant Ask An Expert
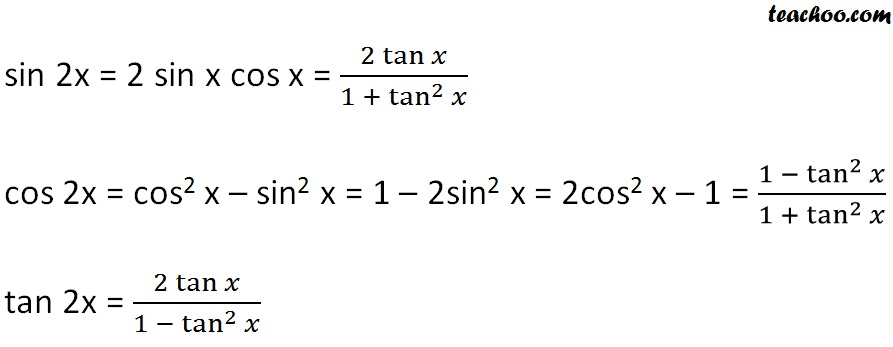



Half Angle Formulas Power Reducing Formulas 2x 3x Formula Provin



What Are The Formulas Of Sin 2x Quora




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities



2




Double Angle Identities Solutions Examples Videos Worksheets Games Activities




Analytic Trig Ppt Video Online Download




Misc 8 Tan X 4 3 Find Sin X 2 Cos X 2 And Tan X 2




Double Angle Formulas What Are Double Angle Formulas Examples
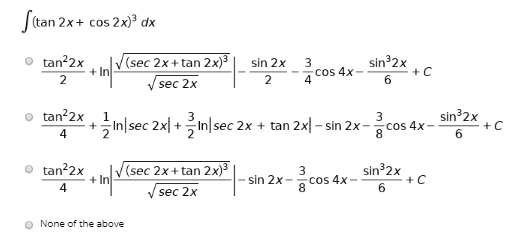



Answered Stan 2x Cos 2x Dx Tan 2x 2 V Sec 2x Bartleby




Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Trig Identity Sec2x Minus Tan2x T10 Youtube




Tan2x ただの悪魔の画像




Solved Problem 4 Using The Sin And Cos Addition Formulas Chegg Com




Ppt Find Sin 2x Cos 2x And Tan 2x From The Given Information Image Select The Correct Answer Powerpoint Presentation Id
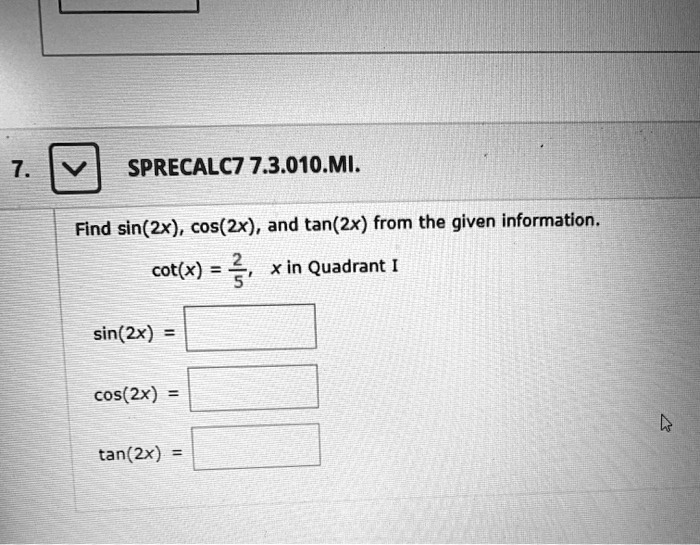



Yewms5xtyqgtbm




Rewrite Sin 2x Tan 2x In Terms Of The First Power Of Cosine Using The Power Reducing Formula Study Com




Fastest Sin2x Identity In Terms Of Tan




Tan2x ただの悪魔の画像




Sin 2x Formula Trigonometry Formula




Write Sin2x As Tanx Q18 P 408 Nelson Youtube



3
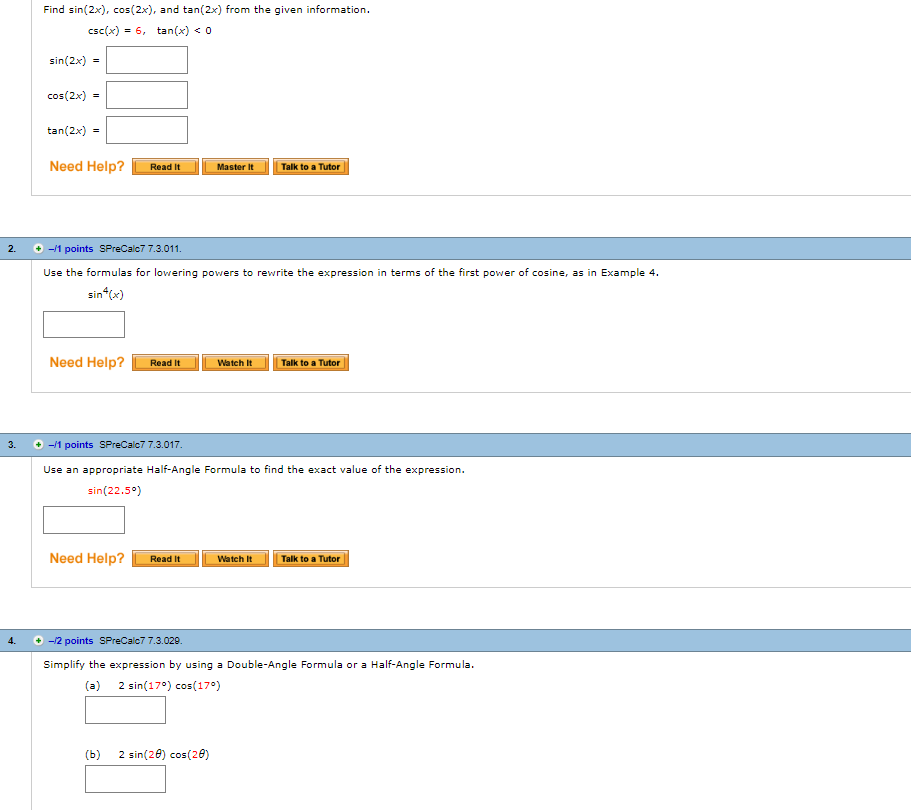



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




Multiple Angle Formulas Es Demonstrating Understanding Of Concepts Warm Up Use A Sum Formula To Rewrite Sin 2x In Terms Of Just Sin X Cos X Do Ppt Download
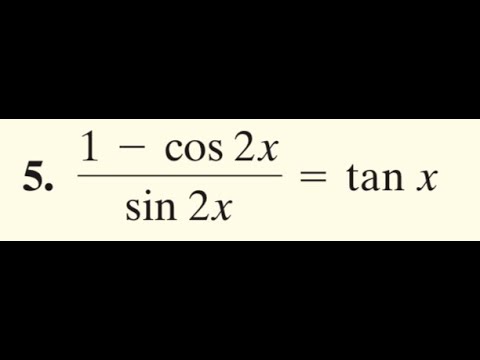



Verify 1 Cos 2x Sin2x Tan X Youtube
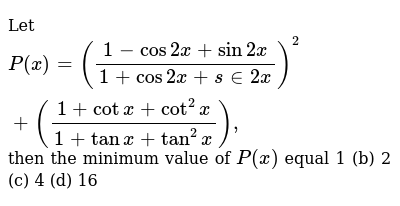



Let P X 1 Cos2x Sin2x 1 Cos2x S In2x 2 1 Cotx Cot 2x 1 Tanx Tan 2x Then The Minimum Value Of P X Equal 1 B 2 C 4 D 16



What Is The Formula Of Tan2x Quora



Sin2x




Sin 2 X Dawonaldson



2
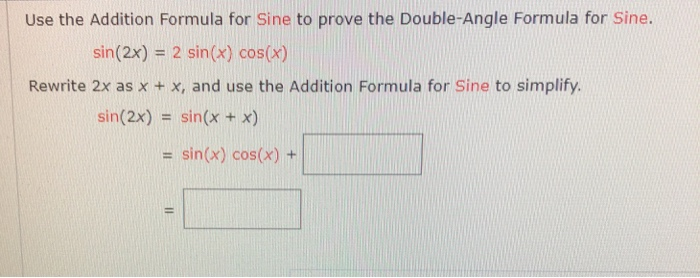



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com



1




Tan 2x Formula What Is Tan 2x Formula Examples




Tan 2x Sin 2x Tan 2x Sin 2x



Tan2x ただの悪魔の画像




How To Write Double Angle Formula Sin 2x In Terms Of Tan X Youtube



Sin 2x Formula Sin 2theta Formula Practice Examples
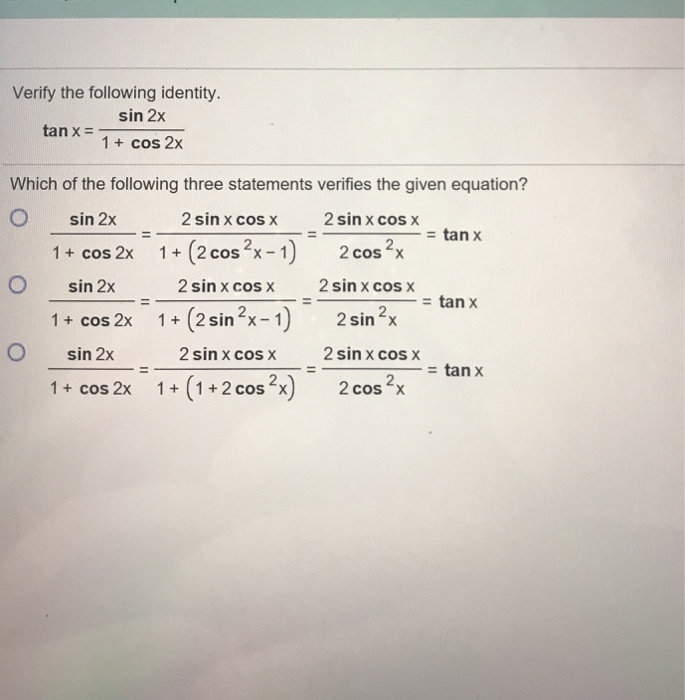



Solved Verify The Following Identity Tan X Sin2x 1 Cos Chegg Com



1
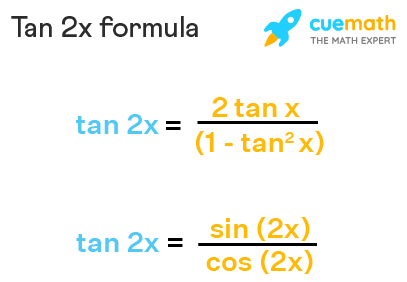



Tan 2x Formula What Is Tan 2x Formula Examples
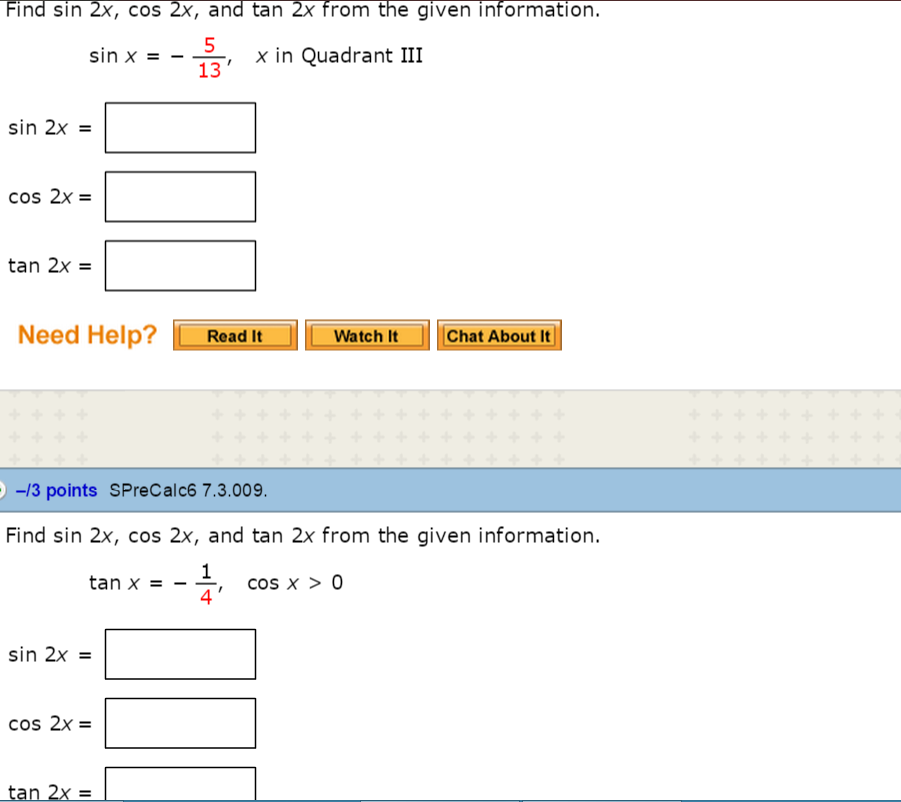



Solved Find Sin 2x Cos 2x And Tan 2x From The Given Chegg Com




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



Tan2x 1 ただの悪魔の画像




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic




Solved Find Sin 2x Cos 2x And Tan 2x If Sinx 13 And X Chegg Com



What Is The Value Of Sin 2x In Terms Of Tan X Quora
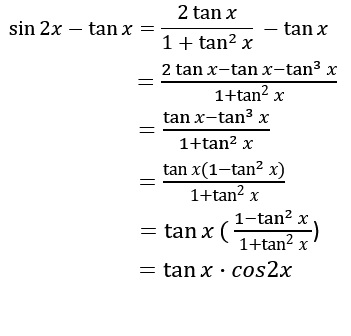



Sin2x Tanx Complete The Identity Socratic



Sin 2x Cos 2x And Tan 2x




Tan2x Sin2x Tan2x Sin2x 5 1 Brainly In




Day 3 Hw 3 To 4 Find Sin2x Cos2x And Tan2x Given One Trig Value And The Quadrant Youtube
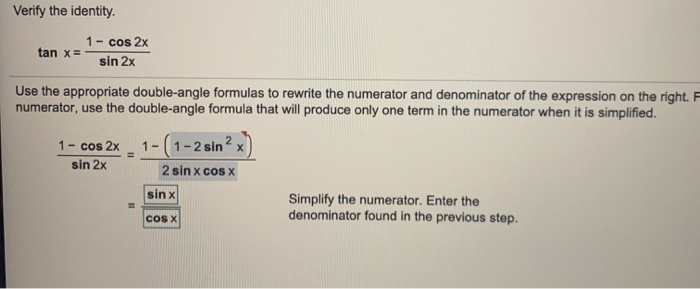



Solved Verify The Identity 1 Cos 2x Tan X Sin 2x Use The Chegg Com




Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube



Prove Sin2x 2tanx 1 Tan 2x Socratic




Lesson 4 5 Double Angle Formulas



0 件のコメント:
コメントを投稿